Все более короткие циклы разработки продукта требуют высокопроизводительных подходов к моделированию и алгоритмов расчета. Подходы расчета FVA Workbench основаны на аналитических методах, которые были созданы в приводной технике на протяжении десятилетий и были подтверждены исследовательскими проектами FVA. Преимущество этих решений - высокая производительность вычислений с очень хорошими результатами
Однако не все тела могут быть описаны аналитически с достаточной точностью. Поэтому в FVA Workbench учитываются, в частности, корпус, держатели планет, колесные тела и валы с использованием метода конечных элементов.
FE для сложных геометрий

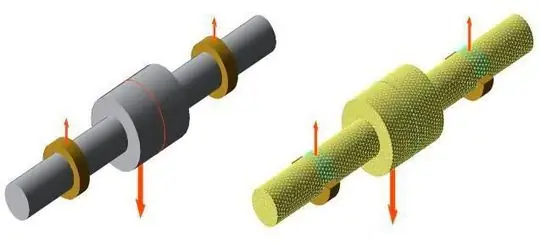
Подход FE обычно подходит для сложных геометрий компонентов, которые больше не могут быть отображены в рамках аналитических подходов (рисунок 1). Это различие объясняется ниже на примере расчета вала, недавно интегрированного в версию 5.6 FVA Workbench с использованием подхода FE.
Расчет волновой деформации
Волновая деформация рассчитывается в FVA Workbench с использованием подхода Тимошенко. В этом подходе деформация изгиба по методу Эйлера / Бернулли объединяется с учетом сдвиговых деформаций. Подход Тимошенко имеет следующие ограничения:
- Площадь поперечного сечения компонента не выпуклая.
- Рассчитаны только вращательно-симметричные компоненты (сплошные и полые валы).
- Конические или изогнутые контуры заменяются ступенчатыми цилиндрическими секциями.
- Силы и моменты вводятся по центральной оси.
- Поток мощности в ступенчатых волнах не учитывается правильно.
При большинстве распространенных геометрий вала эти ограничения не приводят к практическим отклонениям от реальной деформации вала. Однако, если используются более сложные геометрии или если вы хотите проверить, приводят ли ограничения стержня Тимошенко к геометрии вала к заметным отклонениям, FVA Workbench из версии 5.6 также может рассчитывать деформации вала с использованием FEM.
Для этого волны, настроенные в FVA Workbench, могут быть объединены в сеть. С более сложной геометрией, волны, экспортируемые из программ CAD, могут считываться и объединяться в сеть. Сетевое взаимодействие и определение узлов контакта с остальной частью модели передачи в значительной степени автоматическое.
Встреча пользователей технологии мехатронного привода
Основное внимание пользователей, использующих технологию мехатронного привода, уделяется механическим компонентам зубчатых колес, сцеплений и тормозов, а также их конструкции, размерам и взаимодействию в общей мехатронной системе.
Больше информации
К волне FE быстро и качественно
Руководство пользователя было разработано для максимальной эффективности, так что волна FE может быть смоделирована, объединена в сеть и рассчитана в течение очень короткого времени. Для внутренней сети могут использоваться как линейные, так и квадратичные тетраэдрические элементы. Всего несколькими щелчками мыши каждый пользователь может создать полноценную сеть для расчета FE, даже без специальных знаний FE. Это автоматизированное сетевое взаимодействие возможно, поскольку проведенный здесь анализ деформации предъявляет гораздо меньшие требования к тонкости сетки, чем анализ напряжений.
Встреча пользователей технологии мехатронного привода
Ваш путь к эффективной трансмиссии
Пример расчета: сравнение стержня Тимошенко - метод ИП
Разница между расчетом FE и расчетом Тимошенко поясняется ниже с использованием в качестве примера ступенчатого вала. Сравнительный расчет был выполнен на упрощенной геометрии вала (рис. 2). Вал имеет два подшипника и нагружен одним усилием в середине.
- Наружный диаметр среднего сечения вала изменен для сравнительных расчетов.
- Соотношения в диапазоне от 1 (гладкая волна) до 3,5 (очень сильный абзац) варьируются.
- Основной диаметр вала составляет 50 мм.
Метод FE в верстаке FVA
Чтобы связать жесткость элементов КЭ с аналитическими подходами, жесткость сводится к точкам сцепления. В случае вала точки сцепления - это подшипники, шестерни, точки приложения нагрузки или муфты. При уменьшении определяется матрица жесткости для точек связи, которая описывает поведение деформации в точках связи, а также полное рассмотрение всей компоненты КЭ. Поэтому в расчете видны только точки пересечения.
Расчет под воздействием всех деформаций
На этапе последующей обработки деформации всего компонента могут быть рассчитаны с использованием нагрузок на точки соединения. Эта процедура обеспечивает высокопроизводительный расчет под воздействием всех деформаций в трансмиссии. Влияние на зацепление экспериментально продемонстрировано в исследовательском проекте FVA 592 II.
Отклонения двух методов
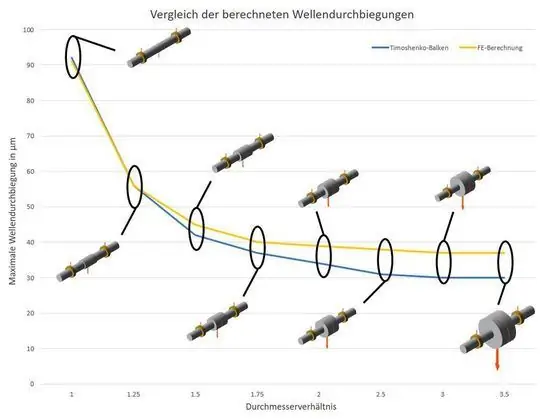
На фиг.3 показана максимальная зенковка вала по отношению наружного диаметра среднего сегмента к диаметру соседних секций вала.
Видно, что для гладкой волны аналитический подход дает тот же результат, что и расчет КЭ. При увеличении диаметра в 1,25 раза аналитическое решение рассчитывает более низкую зенковку для этой геометрии вала, чем расчет FE. Начиная с 3-х кратного увеличения диаметра среднего сечения, расчет КЭ показывает постоянное падение на 23% выше, чем при аналитическом подходе.
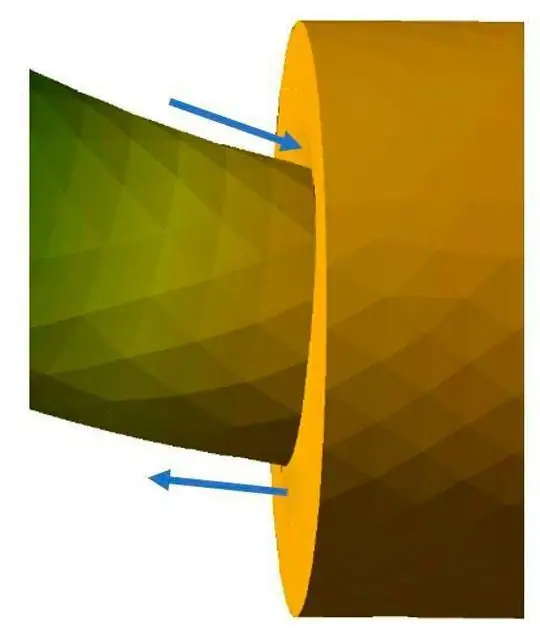
В этом случае разницу можно объяснить двумя причинами: с одной стороны, это связано с неравномерно распределенным потоком силы поперечного сечения, а с другой - с кривизной поперечного сечения вала в области шага диаметра (рис. 4). Как описано выше, эти два эффекта не учитываются в аналитическом подходе Тимошенко.
Разработка снаряжения
Подготовьте сложные расчеты в удобной для пользователя форме
Практический пример
Описанные различия в методе расчета отклонений вала также могут быть определены в практических моделях зубчатых колес, таких как коническое зубчатое колесо, показанное на рисунке 5.

Здесь сначала было выполнено распределение рабочей нагрузки выходного каскада для следующих вариантов промежуточного вала:
- Аналитический расчет всех волн
- ИП расчет промежуточной волны, остальные волны рассчитывались аналитически.
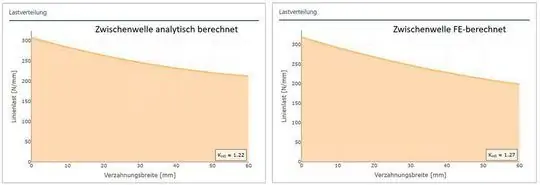
На рисунке 6 показано распределение нагрузки для обоих рассчитанных вариантов. Хотя здесь влияние на прогиб вала не так сильно, как в теоретическом примере на рис. 2, расчет промежуточного вала с FE показывает заметное увеличение коэффициента ширины KHß с 1,22 до 1,27.
Реалистичное представление волн и мировоззрения
Одновременно с реализацией расчета КЭ волн, графическое представление волн в трехмерной модели было значительно улучшено. Начиная с версии 5.6 FVA Workbench, в 3D-модели реалистично отображается подробная геометрия выемок, таких как шпонки, выступы валов с подрезкой и прямоугольные канавки, так что пользователь получает графическую обратную связь по выполненным элементам геометрии (рисунок 7).
Эти усовершенствования также будут реализованы в следующей версии FVA Workbench с целью внедрения руководства FKM для расчета безопасности вала, которое затем дополнит текущий расчет безопасности вала в соответствии с DIN 743.