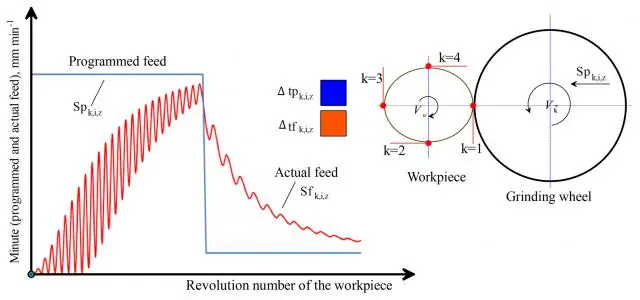
Зубчатые силы приводят к деформации корпусов колес. Это, в свою очередь, влияет на распределение нагрузки на боковой линии, если корпус колеса неравномерно деформируется. На примере простого вала ниже показано влияние деформаций корпуса колеса на распределение нагрузки линейных зубчатых колес.
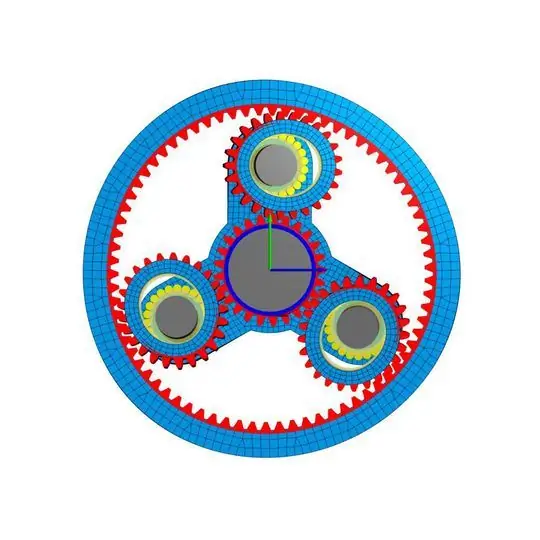
Примером расчета является вал с двумя жесткими опорами, один с центральной шестерней, а другой со смещением для шестерни.
В разделе 7.4.3.2 ИСО 6336-1 предлагается использовать средний диаметр наконечника и корневого круга для расчета деформаций изгиба и диаметра стержня плюс 0,4 * для деформаций кручения. Здесь между ними используется округленное значение 48 мм (z = 25, mn = 2). В разделе 7.4.3.3 в стандарте также указывается, что средний диаметр диаметра отверстия и диаметра ступицы можно использовать для придания жесткости валу посредством зубьев или соединений с запрессовкой. Этот средний диаметр следует использовать только для придания жесткости валу, а не для упругой деформации корпусов колес.
Рассматриваются следующие случаи:
- Расчет с использованием стержневой модели. Диаметр вала в области зубьев увеличивается до диаметра между корнем корня и кончиком.
- Расчет по модели стержня: диаметр вала увеличивается до среднего значения (20 + 48) / 2 = 34 мм.
- Несимметричный 3D-упругий корпус колеса с полотном слева
- 3D эластичный полный цилиндр как корпус колеса
- 3D-эластичный корпус колеса с сеткой посередине
Чтобы рассчитать деформации зубчатых колес, зубчатые колеса сцепляются со вторым жестким центральным колесом. Все образцы валов находятся в зацеплении с центральным колесом и нагружены одинаковым крутящим моментом с левой стороны.

Результаты приведены для центральной передачи и для случая со смещением в следующих обзорах:
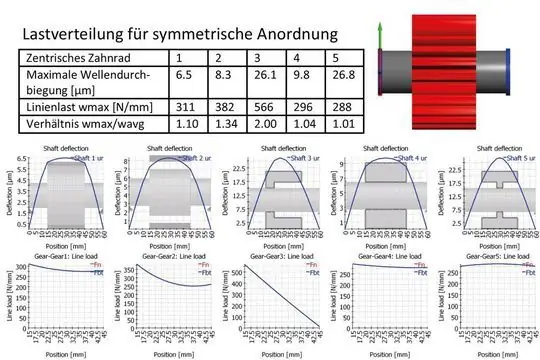
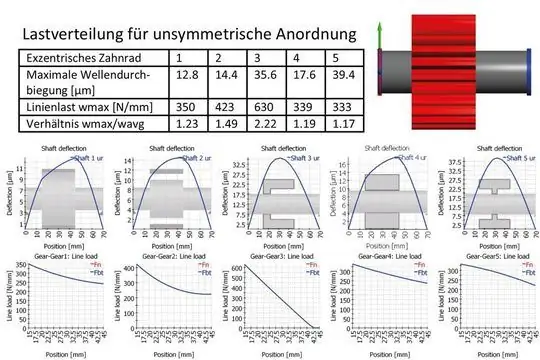
Максимальный прогиб вала указан для внутреннего вала. Отношение wmax / wavg аналогично коэффициенту нагрузки по ширине колесной пары, однако учитываются только зависящие от нагрузки эффекты, а не влияние допусков. Дополнительные производственные допуски или упругость подшипников могут привести к увеличению коэффициента боковой нагрузки.
В корпусах 1 и 4 в качестве корпуса колеса используется сплошной цилиндр. Прогиб вала в случае 4 больше, чем в случае 1, но деформации боковой линии в случае 4 меньше, чем в случае 1. Причина в том, что вал может деформироваться в корпусе колеса. В целом, стержневая модель слишком жесткая в случае изменения поперечного сечения. Трехмерная объемная модель автоматически учитывает распределение напряжений в точке изменения поперечного сечения без необходимости оценивать диаметры жесткости или углы конуса.
Случай 2 со средним диаметром для корпуса колеса бесполезен для расчета деформаций боковых линий, как показывает сравнение со случаями 4 и 5. При запрессовке между валом и корпусом колеса вал становится менее жестким, как в случае 5, где нет жесткости. Тем не менее, в случае 5 очень незначительная деформация боковой линии. Модель расчета со средним диаметром имеет смысл только в том случае, если целью расчета является линия изгиба вала. Отклонение в случае 2 также приближается к случаю 4, хотя это не относится к деформациям боковой линии.
В сравнении случаев 4 и 5, небольшое влияние крутящего момента можно увидеть в распределении нагрузки. В то время как в случае 4 крутящий момент действует слева с полным цилиндром, внешние стороны немного уступают из-за скручивания и изгиба. Это похоже на маленькую корону.
расчет
Как деформация упругого корпуса влияет на распределение нагрузки в подшипнике качения
Случай 3 показывает большое отклонение линии фланга из-за наклона. Основной причиной здесь является не деформация самого корпуса колеса, а сцепление с валом в точке с большим углом наклона. Угол наклона вала и деформация корпуса колеса вносят свой вклад в общее отклонение боковой линии, в то время как в других случаях эффективен небольшой угол наклона вала.
Более детальная модель расчета для корпуса колеса позволяет добиться лучших результатов как для расчета линии изгиба вала, так и для отклонений боковых поверхностей зубьев. В случае расчета с простыми стержневыми элементами наружный диаметр корпуса колеса должен использоваться для расчета деформаций боковых линий. Однако для расчета линии изгиба вала можно использовать меньший диаметр корпуса колеса, который лучше соответствует жесткости вала.
После однократного статического уменьшения корпуса колеса, которое здесь занимает около 1 минуты, расчет занимает всего несколько секунд, как для расчета с элементами стержня. Единственный недостаток трехмерных эластичных компонентов - это увеличение сохраненных файлов вычислений.
В этих примерах не использовалась коррекция зубчатых колес, чтобы показать влияние деформаций на распределение нагрузки на линии. Конечно, расчет также может быть выполнен с коррекцией передач. (Уд)
Видео инструкции о том, как использовать импорт DXF в расчете авторской волны Mesys, можно найти здесь.
* Маркус Раабе, Месис АГ, Цюрих.